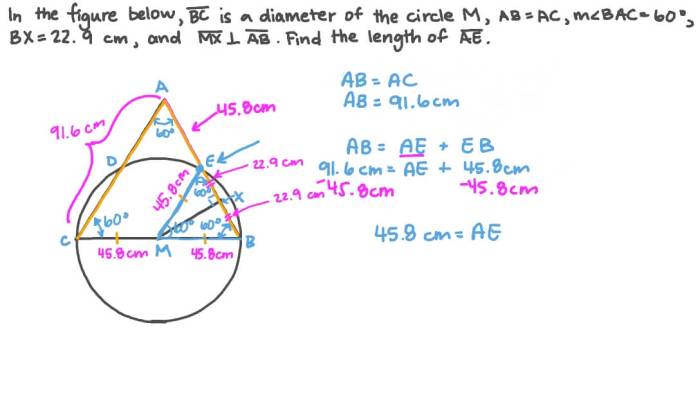
Unveiling the intricacies of geometry, this comprehensive geometry polygon angle measures worksheet embarks on a journey of discovery, empowering learners with the tools to conquer angle measurement challenges within polygons.
Through a series of meticulously crafted problems and interactive explorations, this worksheet unravels the fundamental concepts of polygon angle measures, illuminating the relationship between the number of sides and the sum of interior angles. Dive into a world of polygons, where each angle holds a story, waiting to be deciphered.
Polygon Angle Measures
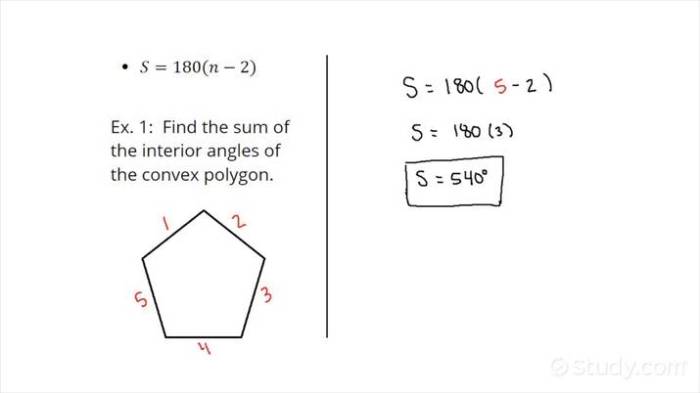
In geometry, a polygon is a closed figure with three or more straight sides. The sum of the interior angles of a polygon is a fundamental property that can be used to identify and classify different types of polygons.
The sum of the interior angles of a polygon is directly related to the number of sides it has. The relationship can be expressed using the following formula:
Sum of Interior Angles = (n
- 2)
- 180 degrees
where n is the number of sides in the polygon.
Examples of Polygons with Different Numbers of Sides and Their Corresponding Angle Measures
- Triangle (n = 3): Sum of interior angles = 180 degrees
- Quadrilateral (n = 4): Sum of interior angles = 360 degrees
- Pentagon (n = 5): Sum of interior angles = 540 degrees
- Hexagon (n = 6): Sum of interior angles = 720 degrees
Polygon Angle Sum Worksheet
A polygon angle sum worksheet is a valuable tool for students to practice calculating the sum of interior angles for different types of polygons.
The worksheet can include a variety of polygons with different numbers of sides. Each problem should provide step-by-step instructions for calculating the sum of interior angles using the formula provided above.
Interactive Angle Measure Exploration, Geometry polygon angle measures worksheet
Interactive angle measure exploration activities allow students to explore the relationship between polygon sides and angle measures in a hands-on manner.
These activities can use simulations or dynamic diagrams to demonstrate how the sum of interior angles changes as the number of polygon sides increases.
Polygon Angle Measure Applications
Polygon angle measures have numerous applications in real-world situations, including:
- Architecture: Determining the angles of roofs and windows
- Engineering: Calculating the angles of bridges and trusses
- Design: Creating patterns and shapes with specific angles
Advanced Polygon Angle Measures
Advanced concepts related to polygon angle measures include:
Exterior Angles
The exterior angle of a polygon is the angle formed by extending one side of the polygon and an adjacent side. The sum of the exterior angles of a polygon is always 360 degrees.
Diagonals
A diagonal is a line segment that connects two non-adjacent vertices of a polygon. The number of diagonals in a polygon can be calculated using the formula:
Number of Diagonals = n(n
3) / 2
where n is the number of sides in the polygon.
Popular Questions: Geometry Polygon Angle Measures Worksheet
What is the formula for calculating the sum of interior angles in a polygon?
The formula is (n-2) x 180 degrees, where n represents the number of sides in the polygon.
How can I use this worksheet to improve my understanding of polygon angle measures?
This worksheet provides a structured approach to practicing angle measurement in polygons, allowing you to reinforce concepts and build confidence.
What are some real-world applications of polygon angle measures?
Polygon angle measures find applications in architecture, engineering, and design, where precise angle calculations are crucial for structural integrity and aesthetic appeal.