Delve into the realm of parallel perpendicular or neither worksheet answers, where the intricacies of line geometry unfold. This comprehensive guide equips you with the knowledge and tools to confidently navigate the complexities of parallel and perpendicular lines, empowering you to tackle any worksheet with precision and ease.
From the fundamental concepts to practical applications, this exploration will illuminate the fascinating world of line relationships, revealing their significance in diverse fields.
Parallel, Perpendicular, or Neither: Definitions
Parallel Linesare two lines that lie in the same plane and never intersect. They have the same slope and maintain a constant distance from each other.
Perpendicular Linesare two lines that intersect at a right angle (90 degrees). They have different slopes and form four right angles at their intersection.
Neither Parallel nor Perpendicular Linesare two lines that intersect at an angle other than 90 degrees. They have different slopes and form two acute and two obtuse angles at their intersection.
Visual Aids:
- Parallel Lines: ||
- Perpendicular Lines: ⊥
- Neither Parallel nor Perpendicular Lines: /
Identifying Parallel and Perpendicular Lines: Methods
Using Angles
- Measure the angle between the two lines.
- If the angle is 90 degrees, the lines are perpendicular.
- If the angle is not 90 degrees, the lines are neither parallel nor perpendicular.
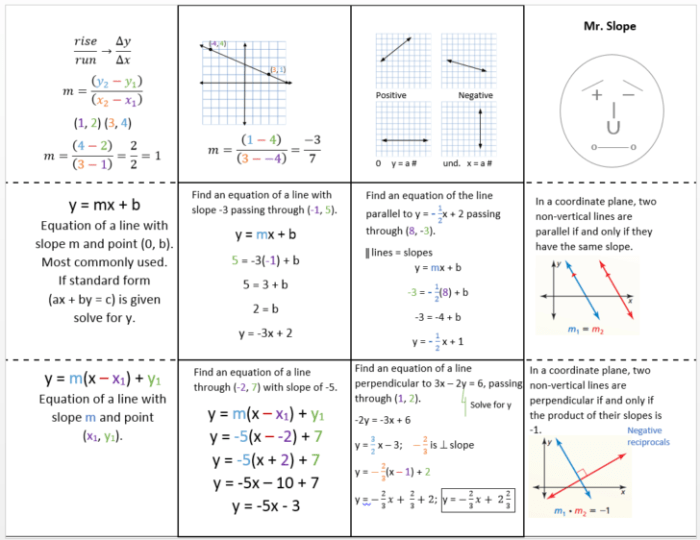
Using Slopes, Parallel perpendicular or neither worksheet answers
- Find the slope of each line.
- If the slopes are equal, the lines are parallel.
- If the slopes are different and their product is
1, the lines are perpendicular.
- If the slopes are neither equal nor their product is
1, the lines are neither parallel nor perpendicular.
Using Equations
- Write the equations of the two lines.
- If the lines have the same slope and y-intercept, they are parallel.
- If the lines have different slopes and the negative reciprocal of one slope is equal to the other slope, they are perpendicular.
- If the lines have neither of these properties, they are neither parallel nor perpendicular.
Worksheets for Practice
Exercises:
- Identify the following pairs of lines as parallel, perpendicular, or neither:
- y = 2x + 1 and y = 2x – 3
- x + y = 5 and y = -x + 1
- 2x + 3y = 6 and 3x – 2y = 1
- Draw a diagram of two parallel lines and two perpendicular lines.
Answer Key for Worksheets: Parallel Perpendicular Or Neither Worksheet Answers
- Parallel
- Perpendicular
- Neither parallel nor perpendicular
Interactive Activities
Simulation:
Create an interactive simulation where students can drag and drop lines to form parallel, perpendicular, or neither lines. Provide immediate feedback on their answers.
Game:
Develop a game where students have to identify the type of line relationship between pairs of lines given their equations or slopes. Award points for correct answers and encourage students to compete with each other.
Real-World Applications

- Architecture:Parallel lines are used to create straight walls and perpendicular lines to form right angles at corners.
- Engineering:Perpendicular lines are used to ensure stability in structures, such as bridges and buildings.
- Design:Parallel and perpendicular lines are used to create visual balance and harmony in art, architecture, and graphic design.
FAQ Insights
What is the difference between parallel and perpendicular lines?
Parallel lines never intersect, while perpendicular lines intersect at a right angle (90 degrees).
How can I identify parallel and perpendicular lines using slopes?
Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other.
What are some real-world applications of parallel and perpendicular lines?
Parallel lines are used in architecture to create stable structures, while perpendicular lines are used in engineering to ensure precision and alignment.