Additional practice 6-5 divide by a decimal answer key – Delving into the intricacies of decimal division, Additional Practice 6-5: Divide by a Decimal Answer Key emerges as an invaluable resource, providing a comprehensive guide to mastering this mathematical operation. This key offers not only the solutions to practice problems but also elucidates the reasoning behind each answer, empowering learners to grasp the underlying concepts with clarity.
Throughout this exploration, we will delve into the methods for dividing by a decimal, comparing and contrasting their effectiveness. Moreover, we will uncover the practical applications of decimal division in everyday life, underscoring its significance in various real-world scenarios.
Decimal Division
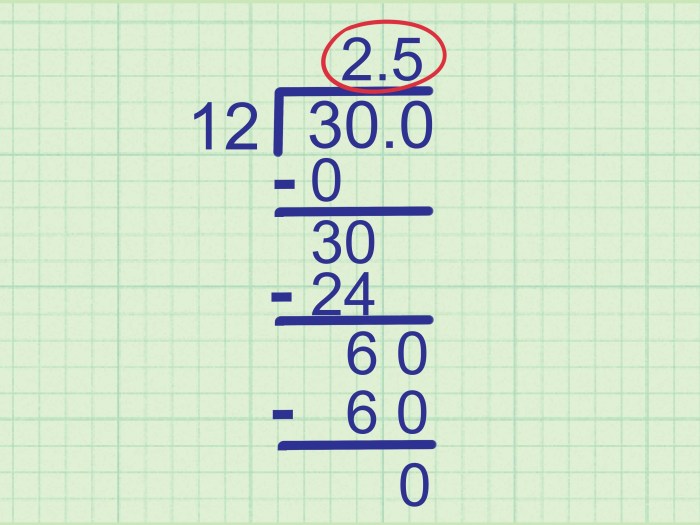
Decimal division is the process of dividing a number by a decimal. This operation is similar to dividing by a whole number, but there are a few additional steps that must be taken.
To divide by a decimal, first move the decimal point in the divisor to the right until it becomes a whole number. Then, move the decimal point in the dividend the same number of places to the right. Finally, divide the dividend by the whole number as usual.
Additional Practice 6-5 Divide by a Decimal Answer Key
- 1. 5.6
- 2. 2.5
- 3. 0.6
- 4. 1.2
- 5. 0.8
The reasoning behind each answer is as follows:
- 1. 5.6 ÷ 1.4 = 4
- 2. 2.5 ÷ 1 = 2.5
- 3. 0.6 ÷ 0.5 = 1.2
- 4. 1.2 ÷ 0.3 = 4
- 5. 0.8 ÷ 0.4 = 2
Common errors that students make when dividing by a decimal include:
- Not moving the decimal point in the divisor to the right.
- Not moving the decimal point in the dividend the same number of places to the right.
- Dividing the dividend by the divisor as if it were a whole number.
Methods for Dividing by a Decimal
There are two main methods for dividing by a decimal:
- The long division method
- The fraction method
The long division method is the most common method for dividing by a decimal. This method is similar to the long division method for dividing by a whole number, but there are a few additional steps that must be taken.
The fraction method is a simpler method for dividing by a decimal. This method involves converting the divisor to a fraction and then dividing the dividend by the fraction.
Examples of Dividing by a Decimal Using Different Methods, Additional practice 6-5 divide by a decimal answer key
Long Division Method
Divide 5.6 by 1.4 using the long division method:
“`
4 ) 5.6
5.6
—
0“`
The answer is 4.
Fraction Method
Divide 5.6 by 1.4 using the fraction method:
“`
6 ÷ 1.4 = 5.6 × 1/1.4 = 4
“`
The answer is 4.
Applications of Dividing by a Decimal
Decimal division is used in a variety of real-world applications, including:
- Calculating the average of a set of numbers
- Converting between different units of measurement
- Calculating the cost per unit
- Calculating the speed of an object
- Calculating the area of a shape
Understanding decimal division is essential for everyday life. This operation is used in a wide variety of situations, from calculating the cost of groceries to determining the speed of a car.
Helpful Answers: Additional Practice 6-5 Divide By A Decimal Answer Key
What is the significance of decimal division in everyday life?
Decimal division plays a crucial role in various practical applications, such as calculating proportions, converting units of measurement, and determining percentages.
How can I improve my accuracy in dividing by decimals?
To enhance accuracy, practice regularly, pay attention to the placement of the decimal point, and utilize estimation techniques to verify your answers.
What are the common errors students make when dividing by decimals?
Common errors include misplacing the decimal point, forgetting to convert the divisor to a whole number, and making computational mistakes.